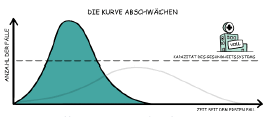
Wie kann man die Kurve abflachen?
Gestern hast Du gesehen wie groß der Unterschied bei der Zahl der angesteckten Menschen ist, wenn man ganz normal lebt im Vergleich zu, wenn man mit den ganzen Einschränkungen lebt. Auch wenn es schwerfällt ist es also sinnvoll, dass Großeltern und Freunde zur Zeit nicht besucht werden. Nun stellt sich die Frage: Wie lange wird das noch so gehen? Leider kann die Frage derzeit niemand beantworten. Allerdings sagt der Virologe (d.h. ein Experte) Christian Drosten, dass die Kurve der Covid-19 Neuansteckungen abgeflacht werden muss. Aber welche Kurve wird da genau betrachtet? Und was bedeutet das „Abflachen“?
Infobox
Welche Kurve abgeflacht werden soll, versteht man, wenn man auf die Seite des Robert Koch-Instituts geht (web-Adresse s. Hinweise). Dort sieht man rechts unten Graphen. Klickt man dort auf „Fälle kumuliert“, dann hat man für jeden Tag die Anzahl derer, die sich bis dahin nachweislich angesteckt haben. Das sind die, die bisher bei unseren Aufgaben betrachtet wurden. Stell Dir vor, Du fährst mit dem Fahrrad auf dieser Kurve von links nach rechts. Zwischen Mitte und Ende März ist die Kurve steiler. Jetzt, Anfang April, verläuft sie flacher. Viel einfacher erkennt man das Abflachen der Kurve aber an den „Fällen/Tag“ (Fälle pro Tag). Was es mit den Fällen/Tag auf sich hat, erfährst Du in der Aufgabe
Begreifen und verstehen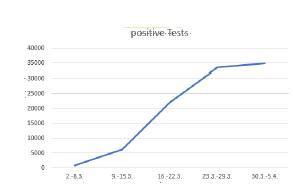
Wie die Kurve für die Fälle pro Tag in der Zeit aussieht, in der sich die Anzahl der nachweislich Angesteckten alle drei Tage verdoppelt soll jetzt an Hand des Schachbretts nachvollzogen werden:
1) Lege die Reiskörner in der ersten Reihe des Schachbretts genauso aus wie bei „Aufgabe 1: Ausbreitung“.
2) In der zweiten Reihe zählst Du nun den Zuwachs an Reiskörner der ersten Reihe. Ein Beispiel ist bei den Bearbeitungshinweisen (s. Hinweise). Was stellt man fest, wenn man die beiden Reihen vergleicht?
Weil die Zahl der positiven Tests innerhalb einer Woche sehr stark schwankt (s. Seite des Robert Koch-Instituts „Fälle/Tag“) ist hier rechts neben „Begreifen und verstehen“ das Schaubild mit Fällen/Woche (Fälle pro Woche). Dies entspricht ungefähr, wenn Du jedes zweite Feld der zweiten Reihe auf Deinem Schachbrett betrachtest. Im Gegensatz zum Schachbrett, wo die Zahlen immer mehr steigen, sieht man bei dem Schaubild ein deutliches Abflachen. Gerade von der vorletzten Woche auf die letzte Woche haben sich die Anzahl der positiven Tests nicht vervielfacht, sondern ist fast gleich geblieben.
Inhaltsbezogene Kompetenzen
