Die Bestimmung der Fläche unregelmäßiger Formen wie Länder und Regionen kann kompliziert sein. Ein 1899 vom österreichischen Mathematiker Georg Alexander Pick (1859–1942) entdeckter Satz kann jedoch dabei helfen, einfache und gute Näherungswerte zu erhalten!
Um den Satz von Pick anzuwenden, benötigt man ein quadratisches Gitter. Die Fläche des kleinsten Quadrats im Gitter wird als quadratische Einheit bezeichnet. Die Menge der Schnittpunkte der Linien, die das Gitter bilden, wird als (quadratisches) Gitter bezeichnet. Der Satz von Pick ist auf jede polygonale Form anwendbar, deren Eckpunkte alle Gitterpunkte sind – ein Gitterpolygon.
Satz von Pick: Bei einem gegebenen Gitterpolygon sei I die Anzahl der Gitterpunkte innerhalb des Polygons und B die Anzahl der Gitterpunkte an seiner Grenze. Dann beträgt die Fläche A des Polygons I + B/2 – 1 Quadrat-Einheiten.
Beispiel 1. Angenommen, das Gitter besteht aus Einheitsquadraten (Seitenlänge gleich 1), dann beträgt die Fläche des blauen Gitterpolygons in der Abbildung rechts 47 + 9/2 – 1 = 50,5, da sich 9 Gitterpunkte auf der Grenze des Polygons (rot markiert) und 47 Gitterpunkte innerhalb des Polygons befinden.
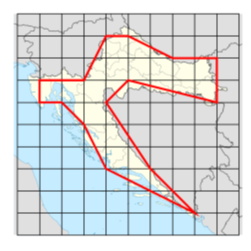
Beispiel 2. Das Bild oben auf dieser Seite zeigt die Karte von Kroatien, überlagert mit einem quadratischen Gitter. Die quadratische Einheit beträgt 2500 km2. Die Form Kroatiens wird durch ein Gitterpolygon (rot) angenähert. Es gibt 20 Gitterpunkte an seiner Grenze und 12 Gitterpunkte im Inneren, sodass seine Fläche nach der Pick-Formel 21 Quadrat-Einheiten beträgt, d. h. 52500 km2 .Beachte, dass wir selbst dann, wenn das Gitterpolygon keine allzu gute Annäherung an die Form Kroatiens war, eine vernünftige Annäherung an die tatsächliche Fläche (56594 km2)) erhalten haben.
Bildquelle: Lizenz CC 3.0 / GNU Free Documentation License, Autor NordNordWest, veröffentlicht auf Wikipedia (https://commons.wikimedia.org/wiki/File:Croatia_location_map.svg).
CC-BY-NC-SA 4.0 Lizenz wird gewährt
Inhaltsbezogene Kompetenzen
