Der beste und der schlimmste Fall der Testszenarien sind in einer realen Umgebung äußerst selten. Reale Fallsituationen können am besten mit Hilfe einer dynamischen Geometriesimulation untersucht werden (Link siehe oben).
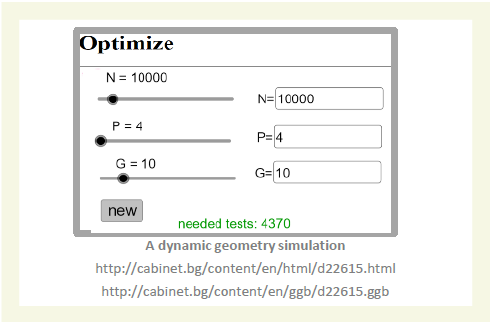
Sei N die Anzahl der Einwohner, P der Prozentsatz der Infizierten und G die Größe der Gruppen von Blutproben, die gemischt werden. Die Simulation prüft, welche der aufeinanderfolgenden Gruppen infiziert sind, und berechnet die erforderliche Anzahl von Tests unter den spezifischen Werten von P, N und G und der gewollt „zufälligen“
Mischung der infizierten ( (𝑃 ∙ 𝑁)/100 ) Blutproben.
Wenn wir die Simulation mehrere Male mit den gleichen Werten von N, P und G (immer wieder auf „new“ klicken) ausführen, könnten wir den durchschnittlichen (mittleren) Wert für die Anzahl der notwendigen Tests ermitteln.

Wie hoch ist der Mittelwert der erforderlichen Anzahl von Tests, wenn:
• N = 10 000, P = 4% und G = 10?
• N = 10 000, P = 4% und G = 11?
• N = 10 000, P = 4% und G = 9?
Wie groß sollte die Gruppengröße G sein, damit der Mittelwert der erforderlichen Tests minimal ist, wenn N = 10 000 und P = 4%?
Wenn wir über 10 000 Testkits verfügen und davon ausgehen, dass 4% der Bevölkerung infiziert sind, welche Gruppengröße G der vermischten Blutproben würden wir wählen, um die Anzahl der getesteten Personen zu maximieren?
Inhaltsbezogene Kompetenzen
